On the conservation of BMS-supertranslation through spatial infinity
Abstract
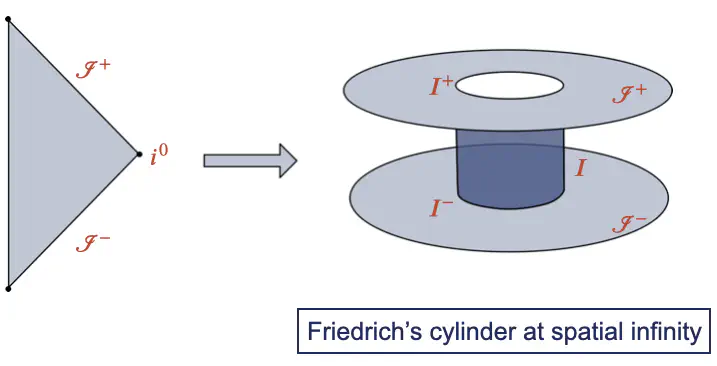
Strominger’s conjecture proposes that BMS-supertranslations and their associated charges at past null infinity are related to those at future null infinity by an antipodal map at spatial infinity. In this talk, I will discuss this conjecture from an initial value perspective using Friedrich’s formulation of spatial infinity. A central structure in this approach is the “cylinder at spatial infinity” which meets past and future null infinities at the so-called critical sets. I will explain how this framework allows us to show that, for a generic class of initial data, the conjecture fails: the BMS-supertranslation charges are not well defined at the critical sets. I will also discuss how imposing additional regularity conditions on the initial data implies well-defined charges and leads to their conservation.