A hyperboloidal method for numerical simulations of multidimensional nonlinear wave equations

Abstract

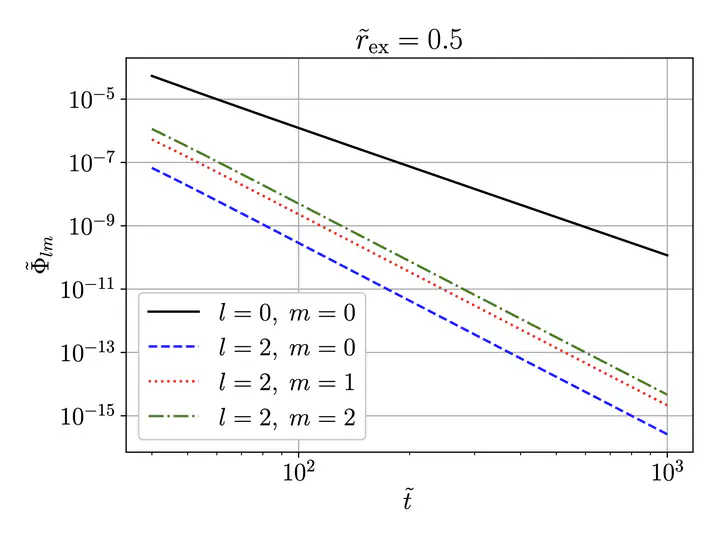
We consider the scalar wave equation with power nonlinearity in $n+1$ dimensions. Unlike most previous numerical studies, we go beyond the radial case and do not assume any symmetries for $n=3$, and we only impose an $SO(n-1)$ symmetry in higher dimensions. Our method is based on a hyperboloidal foliation of Minkowski spacetime and conformal compactification. We focus on the late-time power-law decay (tails) of the solutions and compute decay exponents for different spherical harmonic modes, for subcritical, critical and supercritical, focusing and defocusing nonlinear wave equations.

Oliver Rinne

Professor of Physics