Abstract
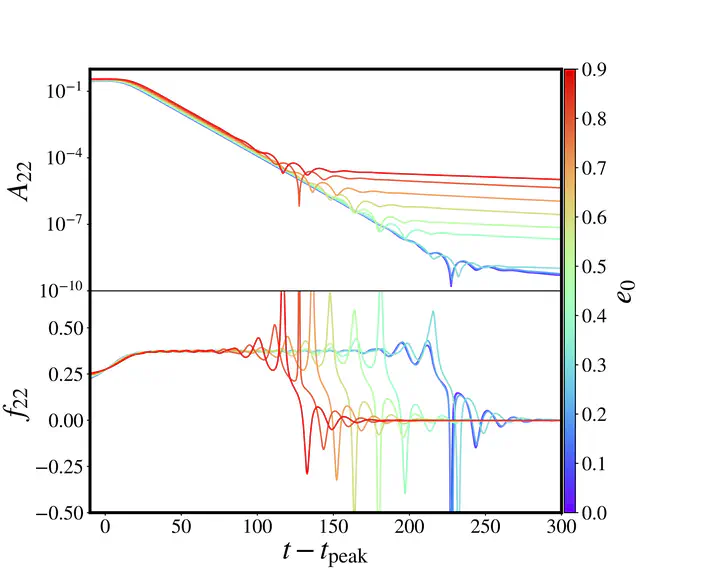
Recently, studies on numerical evolutions of eccentric binary inspirals found a several orders of magnitude enhancement of the post-ringdown tail amplitude. This characteristic might render the tail a phenomenon of observational interest, opening the way to experimental verification of this general relativistic prediction in the near future. I will present an analytical perturbative model that accurately predicts the numerically observed tail evolution.
Considering a source term describing an infalling test-particle in generic non-circular orbits, driven by post-Newtonian radiation reaction, I derive an integral expression over the system's entire history, showing how the post-ringdown tail is inherited from the non-circular inspiral in a non-local fashion. Beyond its excellent agreement with numerical evolutions, the model explains the tail amplification with the progenitors' binary eccentricity.
I will prove the tail to be a superposition of many power-laws, with each term's excitation coefficient depending on the specific inspiral history. A single power law is recovered only in the limit of asymptotically late times, consistent with Price's results and the classical soft-graviton theorem. I will conclude by discussing future directions, including new results for the non-linear extension to equal masses.