Arbitrarily long-lived linear black hole perturbations

Abstract

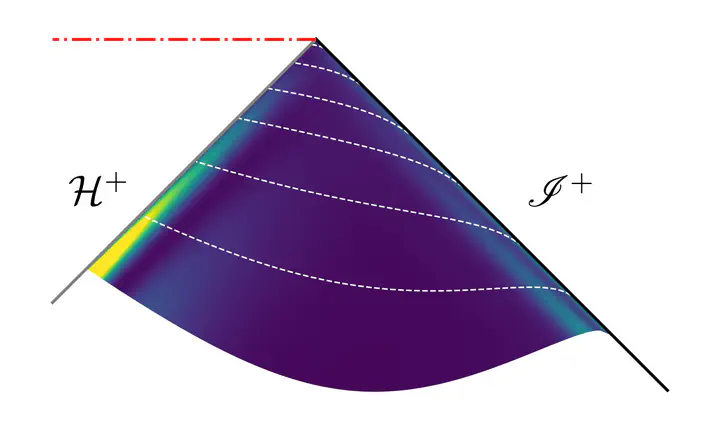
Quasinormal modes (QNMs) of black holes are governed by a non-normal Hamiltonian with respect to a natural choice of inner product, and thus do not form a complete and orthogonal basis. I will show that non-orthogonality leads to the existence of arbitrarily long-lived linear perturbations constructed from finite sums of M QNMs, whose lifetimes scale as log(M). Such perturbations are realised as localised energy packets travelling along the future horizon (and future null infinity). I will discuss simple analytical examples for a massive scalar field in the static patch of de Sitter, as well as numerical examples for gravitational perturbations in the Schwarzschild black hole, using hyperboloidal foliations.

Javier Carballo