Abstract
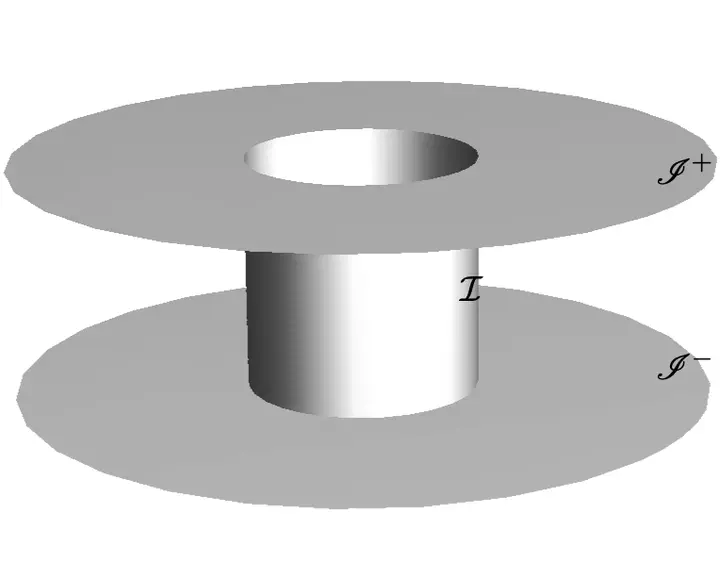
In this overview talk, I will discuss the relation between the asymptotic behaviour of the gravitational at null infinity and spatial infinity, the so-called problem of spatial infinity. I will argue that the conditions assumed by Penrose in his programme to study isolated systems in General Relativity are too restrictive to describe generic spacetimes. I will also discuss how a conformal approach to the study of the structure of spatial initiated by H. Friedrich offers the tantalising possibility of settling down the problem of spatial infinity, thus providing us with a full understanding of the way that Cauchy data determines the asymptotic behaviour of the gravitational field. I will present some applications of these ideas to the computation of asymptotic charges.