Abstract
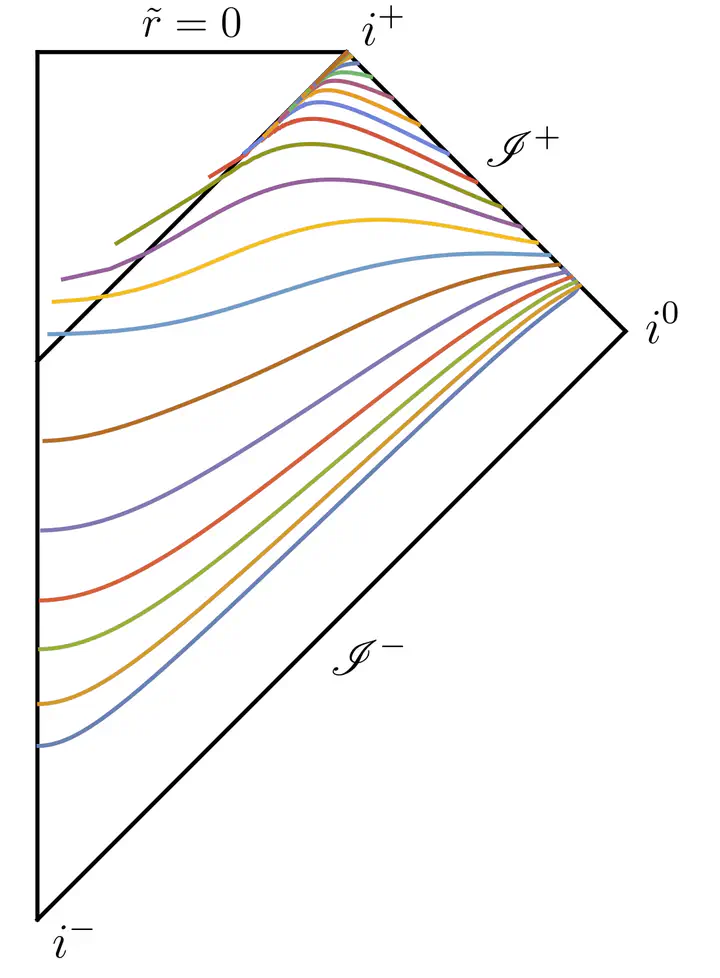
Conformal Carter-Penrose diagrams are a useful tool to understand the causal properties of spacetimes. Here they will be applied to the the visualization of hyperboloidal slices including a black hole. For time-independent slices of the Schwarzschild geometry, the focus will be on the integration of the height function. Slices can be evolved numerically using the eikonal equation, for which I will show diagrams depicting the relaxation of Schwarzschild trumpet slices and the collapse of a massless scalar field into a black hole. Based on the recent preprint.
Date
Fri, 12 Jan 2024 14:00 UTC
Event
Location
Online
Alex Vañó-Viñuales
Post-Doc FCT
Numerical relativist at the interface with mathematical General Relativity.